Select a few x values, and plug them into the equation to find the corresponding y values The x values should be selected around the vertex Tap for more steps Replace the variable x with 0 in the expression f ( 0) = ( ( 0) 3) ( ( 0) 1) Simplify the resultFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorGraph f(x)=x1 Rewrite the function as an equation Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Find the values of and using the form

3 4 Graphs Of Polynomial Functions Mathematics Libretexts
F(x)=1/3x graphed
F(x)=1/3x graphed-Graphing cubic function using translation of y=x^3Graph f (x)=1 f (x) = 1 f ( x) = 1 Rewrite the function as an equation y = 1 y = 1 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the



1
Zeros, End Behavior, and Turning Points Graphs behave differently at various x intercepts Sometimes, the graph will cross over the horizontal axis at an intercept Other times, the graph will touch the horizontal axis and bounce off Suppose, for example, we graph the function f ( x) = ( x 3) ( x − 2) 2 ( x 1) 3 For each zero, state whether the graph crosses the xaxis or touches the xaxis and turns around f(x)=5(x2)(x4)^3 I am having trouble with Math compare the parent function f(x)=x^2 to the quadractic function f(x)=2x^26 the 6 in the function does which of the following?Consider the exponential function f(x) = 3(1/3)^x and its graph Which statements are true for this function and graph?
We are given the function {eq}f(x) = \dfrac{1}{3} x4 {/eq} The given function is a linear function The graph of the linear function would be aAnswer to Let f (x) = 5 x^{1 / 3} x^{5 / 3} Find the intervals of concavity and the inflections point(s) Graph the function By signing up, A positive value of m in the original equation means the graph has a "V" shape, while a negative value of m means the graph has an "upsidedown Vshape" (h,k) is the vertex The vertex is shifted horizontally by h units and vertically by k units f(x)=2abs(x1)3 In this example, m=2 is positive, and the graph will have a Vshape
Please Subscribe here, thank you!!!Answer by Boreal() (Show Source) You can put this solution on YOUR website!Graph {eq}f(x) = 3^x 1 {/eq} Graph The graph of an exponential function shows how rapidly the function increases as its input value increases Even for small changes in the input, the function
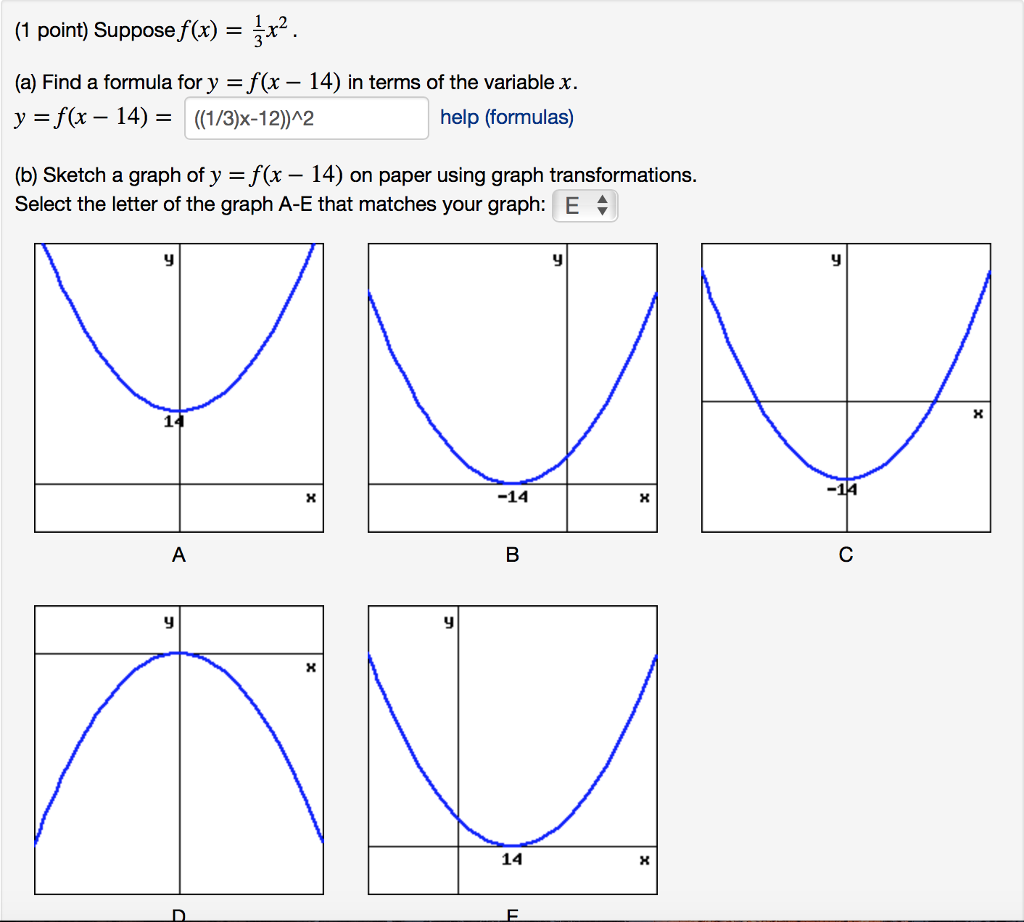



Suppose F X 1 3 X 2 A Find A Formula For Y Chegg Com




3 4 Graphs Of Polynomial Functions Mathematics Libretexts
Graphs of Rational Functions Use the graph of f (x) to explain the relationship between the real zeros of f (x) and its intercept (s) D f (x) has one real zero at 4 because the graph of the function has an intercept at (4, 0)1) f(x)2 A) ( 8x) 2) 3f(x)B)1 3x 8 3) f(x)C)x8 2 4) f(x ) D) x 2 5) 1 3f(x)E)(x 3) 8 6) f(3x) F) 8x 7) f(x) G)(x2) 8) f(x) H) (3x)8 9) f(x2) I)3x8 10) f(x 3) J) (x2)8 For #11 and #12, suppose g(x)=1 x Match each of the numbered functions on the left with the lettered function on the right that it equals 11) 4g(3x7Graph f(x)=(1/3)x Rewrite the function as an equation Rewrite in slopeintercept form Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Reorder terms Use the slopeintercept form to find the slope and yintercept Tap for more steps



Solution Use A Table Of Values To Graph F X And G X On The Same Set Of Axes Graphs Should Be Neatly Labelled A F X 3 To The Power Of X And G X



Search Q X 5e1 3 Graph Tbm Isch
The graph of a function f is the set of all points in the plane of the form (x, f(x)) We could also define the graph of f to be the graph of the equation y = f(x) So, the graph of a function if a special case of the graph of an equation If you want to see a graphCheck all that apply The growth value of the function is 1/3 The function shows exponential decay The function is a stretch of the function f(x) = (1/3)^xF ( x) = 3 x 3 − x 2 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 2 and q divides the leading coefficient 3 One such root is 1 Factor the polynomial by dividing it by x1 Polynomial 3x^ {2}3x2 is not factored since it does not have any rational roots




Consider The Exponential Function F X 3 1 3 X And Its Graph Which Statements Are True For This Brainly Com



Graphs Of Exponential Functions Precalculus
Graph f(x)=x^31 Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Raise to the power of Subtract from The final answer is Convert to decimal Find the point at Tap for more stepsGraph f(x) = 2x 1 − 3 State the domain, range, and asymptote Solution We have an exponential equation of the form f(x) = bx c d, with b = 2, c = 1, and d = −3 Draw the horizontal asymptote y = d , so draw y = −3 Identify the shift as (− c, d), so the shift is (− 1, −3)1 Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of



Solutions 22 Graphs Of Exponential Functions Precalculus I



Confidential 1 Transforming Quadratic Functions Confidential 2 Warm Up Graph Each Quadratic Function 1 Y 2x Y X 2 2x 2 3 Y 3x Ppt Download
Even a function with a smooth graph is not differentiable at a point where its tangent is vertical For instance, the function given by f(x) = x 1/3 is not differentiable at x = 0 In summary, a function that has a derivative is continuous, but there are continuous functions that do not have a derivative Graph of y=(x^31)/(x^24) graph{(x^31)/(x^24) 40, 40, ,} There is no secret to graph a function Make a table of value of f(x) and place points To be more accurate, take a smaller gap between two values of x Better, combine with a sign table, and/or make a variation table of f(x) (depending on your level) Before to start to draw, we can observe some things on f(x) Key point of f(xLet us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;




Let F X 0 If X 3 2 If 3 Lessthanorequalto X Chegg Com



Business Calculus
#color(blue)("Explaining what each part of the equation does")# #color(blue)("ie the transformation from basic form")# This is transforming the graph of #y=x# which is the general shape of the sloping line type / Using the absolute format #y=x # changes the general shape to V where the vertex ( point ) is at the xaxis So for #ul("this case")# Assign a number to x to find f(x) If x is 1, f(x)=3 If x is 2, f(x) = 35 etc Note that f(x) is not defined when x=0 graph{(1/x)4 10, 10, 5, 5} The graph of a quadratic function is called a parabola When a > 0, the parabola opens upward, resulting in a vertex that is a minimum When a < 0, the parabola opens downward, resulting in a vertex that is a maximum The value c is the yintercept of the graph, because a yintercept is a point on the graph where x is zero
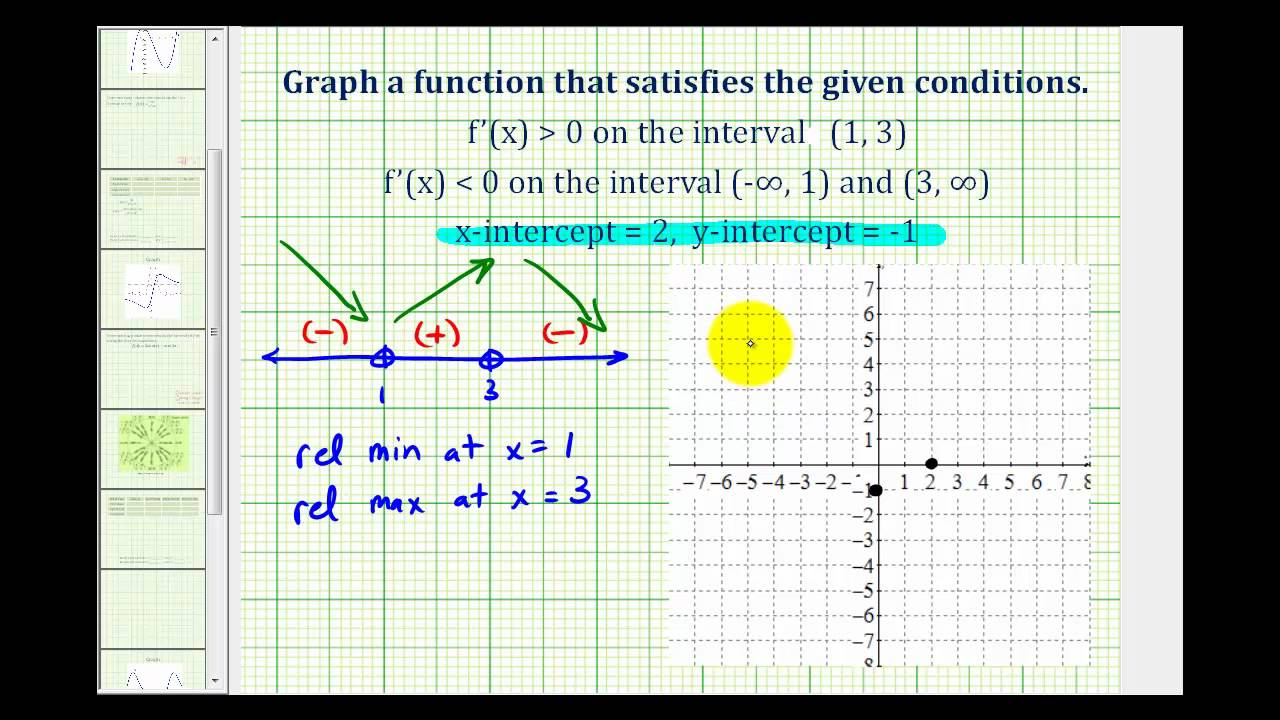



Ex 2 Sketch A Graph Given Information About A Function S First Derivative Youtube
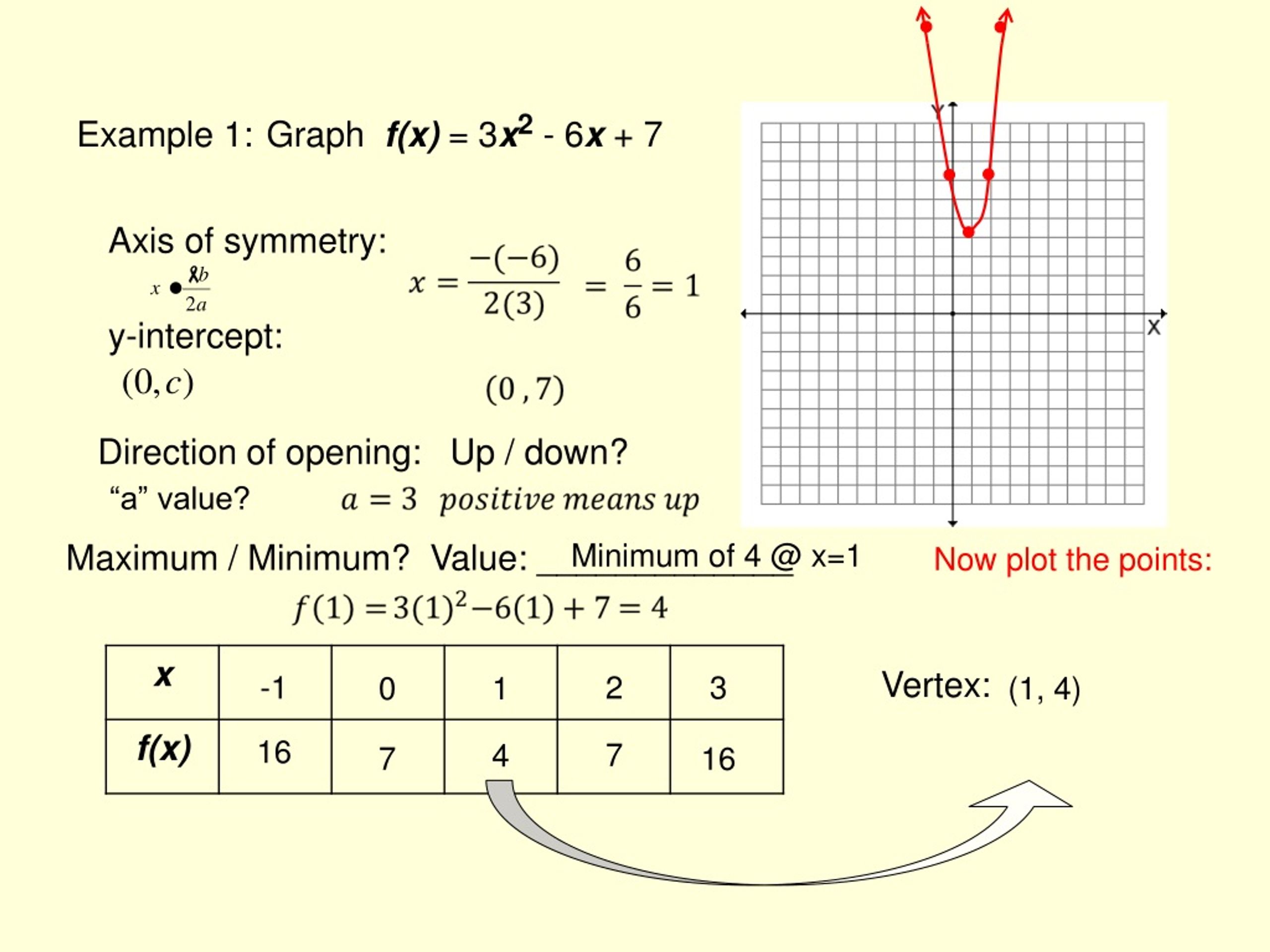



Ppt Algebra 2a Unit 2 Powerpoint Presentation Free Download Id
Horizontal Transformations HI) = 3" 1 f(x) = 3H "The graph was horizontally shifted to the right by 2 units" Vertical Transfonnafians f(x) = 3H 1 fix} = 4(3)"—2 "The graph was vertically stretched by a factor of 4" f0?) = 4'13"" 1 966) = 4(3)"'2 5 "The graphCos(x^2) (x−3)(x3) Zooming and Recentering You can clickanddrag to move the graph around If you just clickandrelease (without moving), then the spot you clicked on will be the new center To reset the zoom to the original click on the Reset button Using "a" ValuesThe domain of f is the range of f 1 and the range of f is the domain of f1 Graph of the Inverse Function The inverse of a function differs from the function in that all the xcoordinates and ycoordinates have been switched




Use The Graph Of F X And G X To Evaluate F G 1 Mathematics Stack Exchange



1
Use opposite sign for horizontal shifts so 3x4Ait makes the graph narrower than the parent function bit makes theSteps Using Derivative Rule for Sum f ( x ) = 3 x ^ { 2 } 1 f ( x) = 3 x 2 1 The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0 The derivative of ax^ {n} is nax^ {n1} The derivative of a polynomial is the sum of
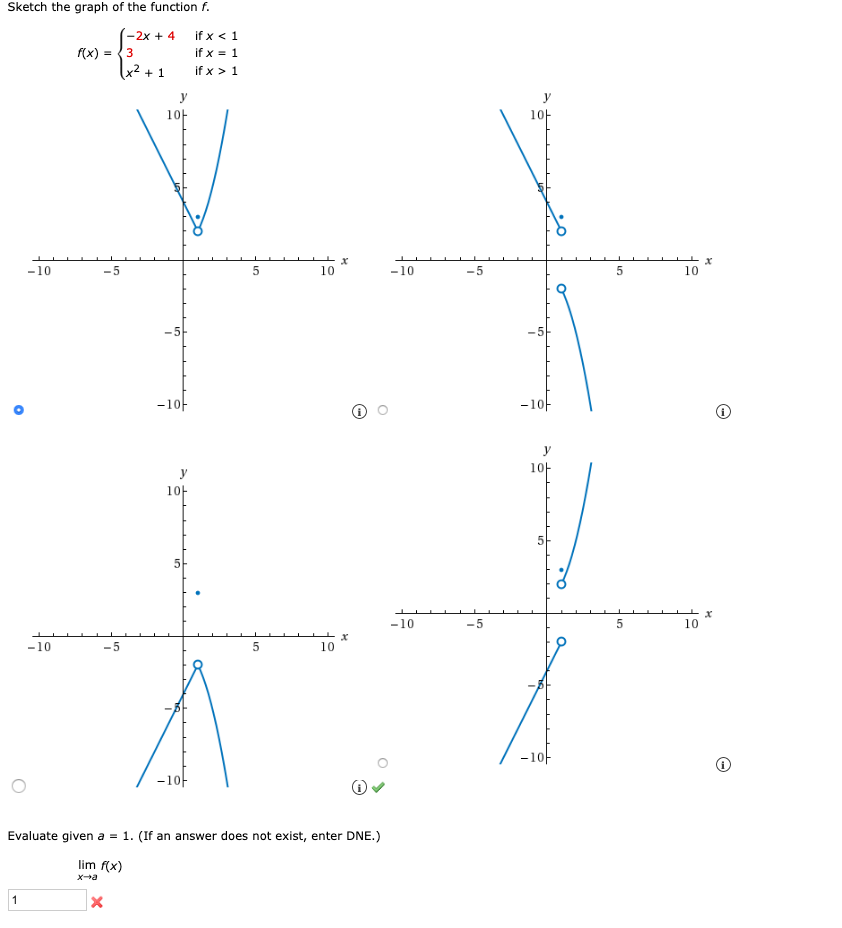



Answered Sketch The Graph Of The Function F Bartleby
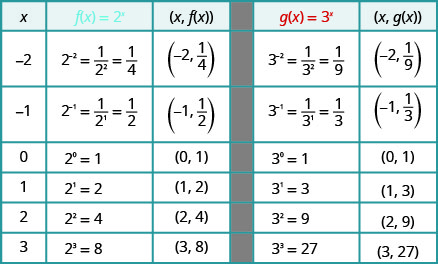



10 3 Evaluate And Graph Exponential Functions Mathematics Libretexts
To find the value of f (3) we need to follow the below steps Step 1 First plot the graph of f (x) Step 2 We need to find f (3) or the function value at x = 3 therefore, in the graph locate the point (3,0) Step 3 Draw a line parallel to Yaxis passing through the point (3,0)In this math video lesson I review how to graph the exponential equation y=2^x by making a table The table helps when graphing these types of equations #eQuestion 1 Graph f(x) = (x 3) – 2 using transformations 2 For the polynomial function g(x) = 2x 5x – 28x – 15, (a) Determine the maximum number of real zeros that the function may have (b) List the potential rational zeros (c) Determine the real zeros of g Factor g over the reals (d) Find the xand yintercepts of the graph of g
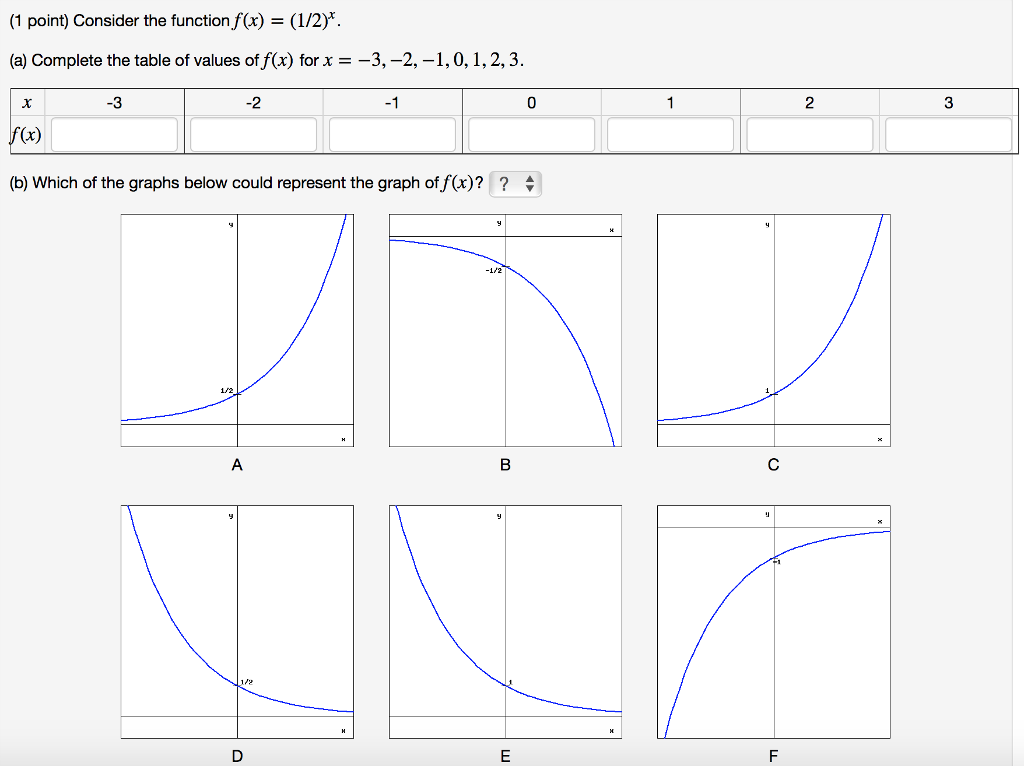



Consider The Function F X 1 2 X A Complete Chegg Com
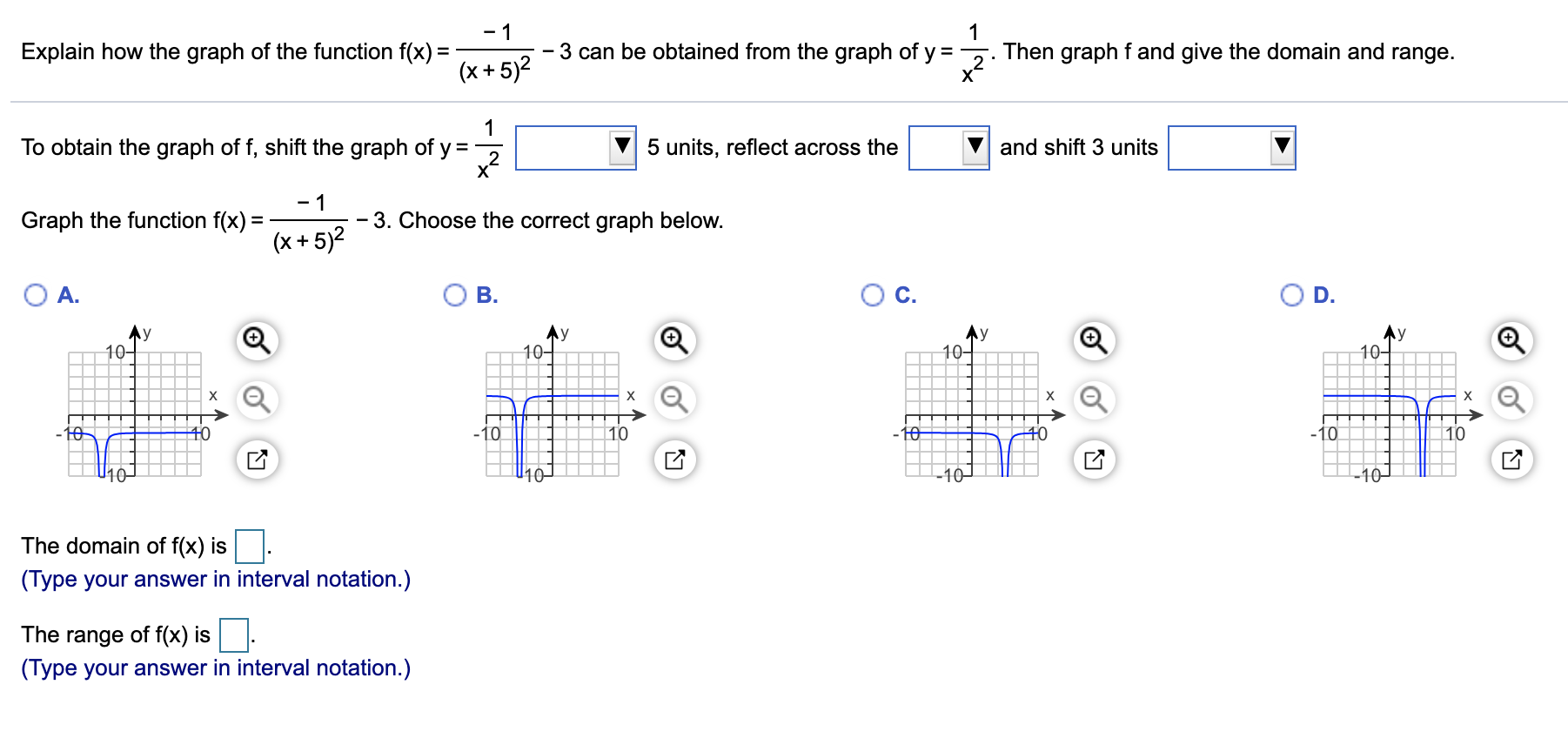



Answered 1 3 Can Be Obtained From The Graph Bartleby
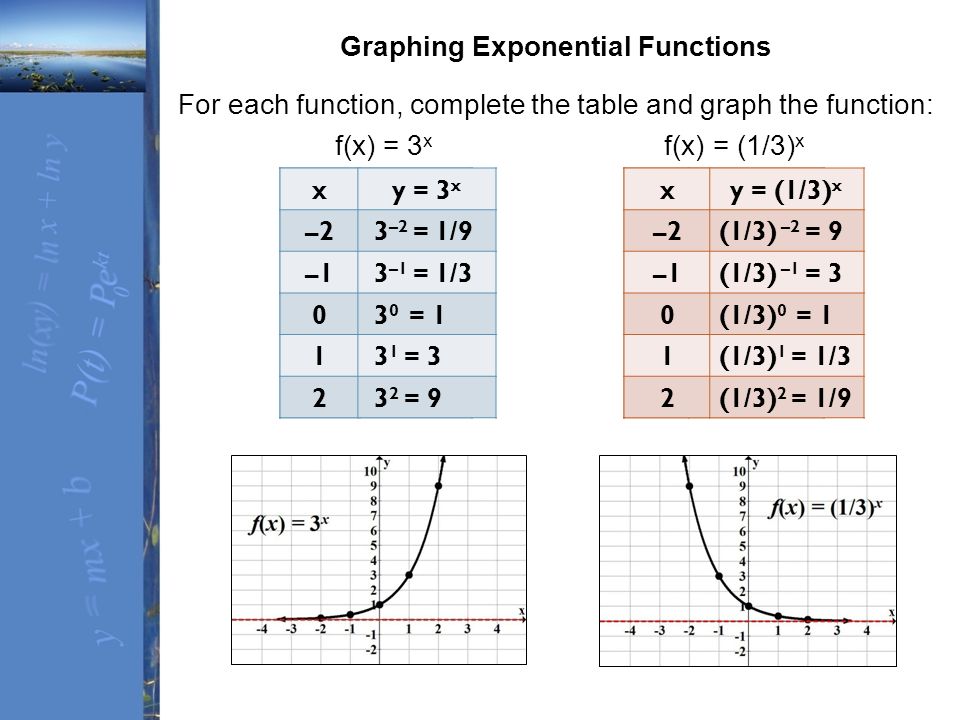
C < 0 moves it down see explanation to sketch f(x) = 3^x choose appropriate values for x and substitute them into the function to obtain corresponding value of y Then plot these coordinate points on squared paper f(0) = 3^0 =1 f(1) = 3^1 = 3 f(2) = 3^2 = 9 f(3) = 3^3 = 27 Now you can plot the points (0 ,1 ) , (1 , 3 ) , (2 , 9 ) and (3 , 27 ) There are also negative values of x that can be F(x) = f(x) − k Table 251 Example 251 Sketch the graph of g(x) = √x 4 Solution Begin with the basic function defined by f(x) = √x and shift the graph up 4 units Answer Figure 253 A horizontal translation 60 is a rigid transformation that shifts a graph left or right relative to the original graph
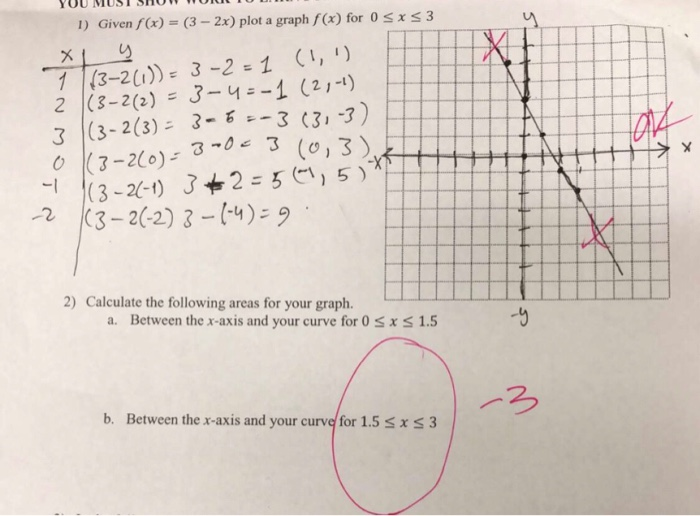



1 Given F X 3 2x Plot A Graph F X For 0 Sxs3 Ex Chegg Com
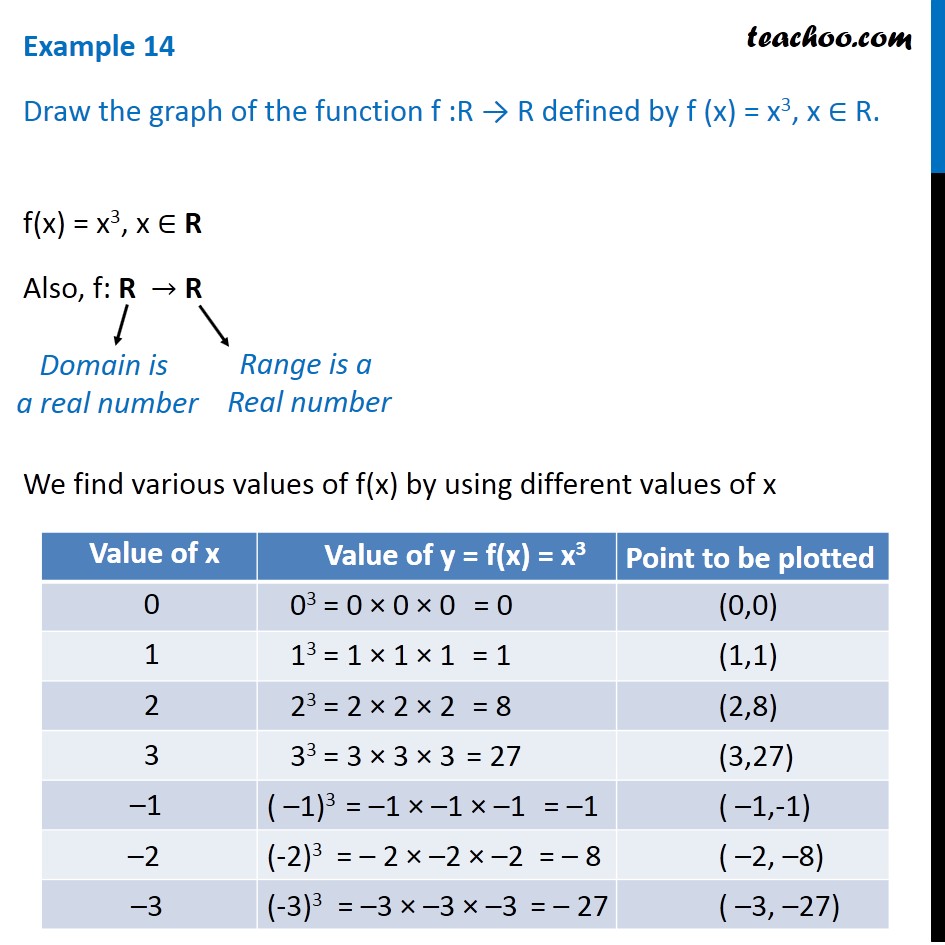



Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11
One way to do this is find any two distict points on the graph then draw a straight line through them Since f (0) = − 1 2(0) 3 = 3 and f (2) = − 1 2(2) 2 = 2, the point (0,3) and (2,2) are on the graph (Note You can also use intercepts) So, by plotting those points and drawing a straight line through them,//googl/JQ8NysUse the Graph of f(x) to Graph g(x) = f(x) 3 MyMathlab HomeworkGraph the exponential problem F(x)=3 x Hi Jose, Set up b and extend the table to x F(x) 1 3 1 = 3 2 3 2 = 9 3 3 3 = 271 31 = 1/32 32 = 1/93 33 = 1/27 Also 3
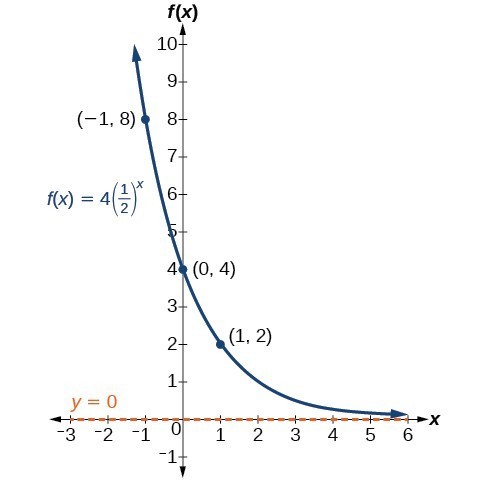



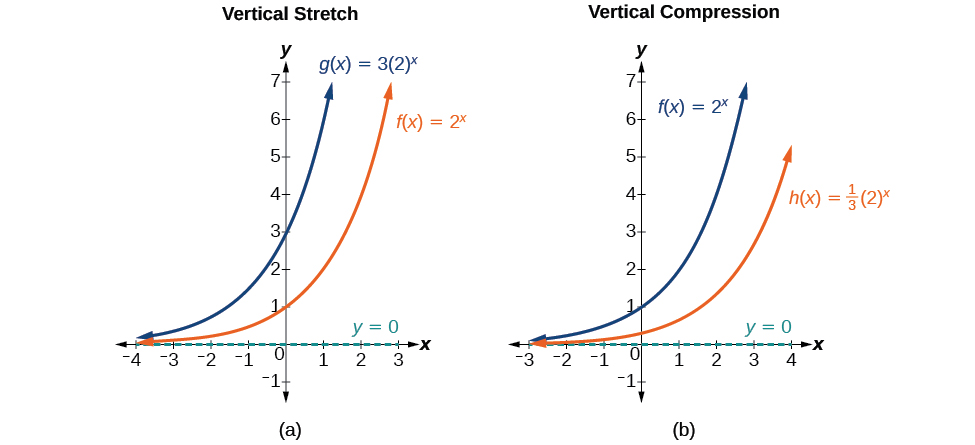
Stretching Compressing Or Reflecting An Exponential Function College Algebra



Solution F X 1 3 X What Would The Domain And Range Of This Function Be I Am Guessing That There Is One Asymptote Y 1 3 So Only The Range Has A Restriction
Use a graph of f(x) to determine the value of f(n), where n is a specific xvalueTable of Contents0000 Finding the value of f(2) from a graph of f(x)002We hope it will be very helpful for you and it will help you to understand the solving process If it's not what You are looking for, type in into the box below your own function and let us find the graph of it The graph of f (x)=1/x3 is a visual presentation of the function in the plane On the given graph you can find all of the important points for function f (x)=1/x3 (if they exist)Graph f(x)=x13 Find the absolute value vertex In this case, the vertex for is Tap for more steps To find the coordinate of the vertex, set the inside of the absolute value equal to In this case, Add to both sides of the equation Replace the variable with in the expression




What Is The Equation Of The Function Shown In The Graph Given That The Equation Of The Parent Brainly Com



Www Lcps Org Cms Lib Va Centricity Domain 3665 Unit 4 day 7 notes a2 Pdf
Graph f(x)=3x1 Rewrite the function as an equation Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is , where is the slope and is the yintercept Find the values of and using the formThese two numbers are the x and y coordinates, respectively, of a point on the graph on f(x) Since zero and negative exponents can be tricky, I will do a couple of these for you For x = 0 Since any nonzero number to the zero power is one we get f(0) = 1 So we have the point (0, 1) when x = 0Please help me on this one!!
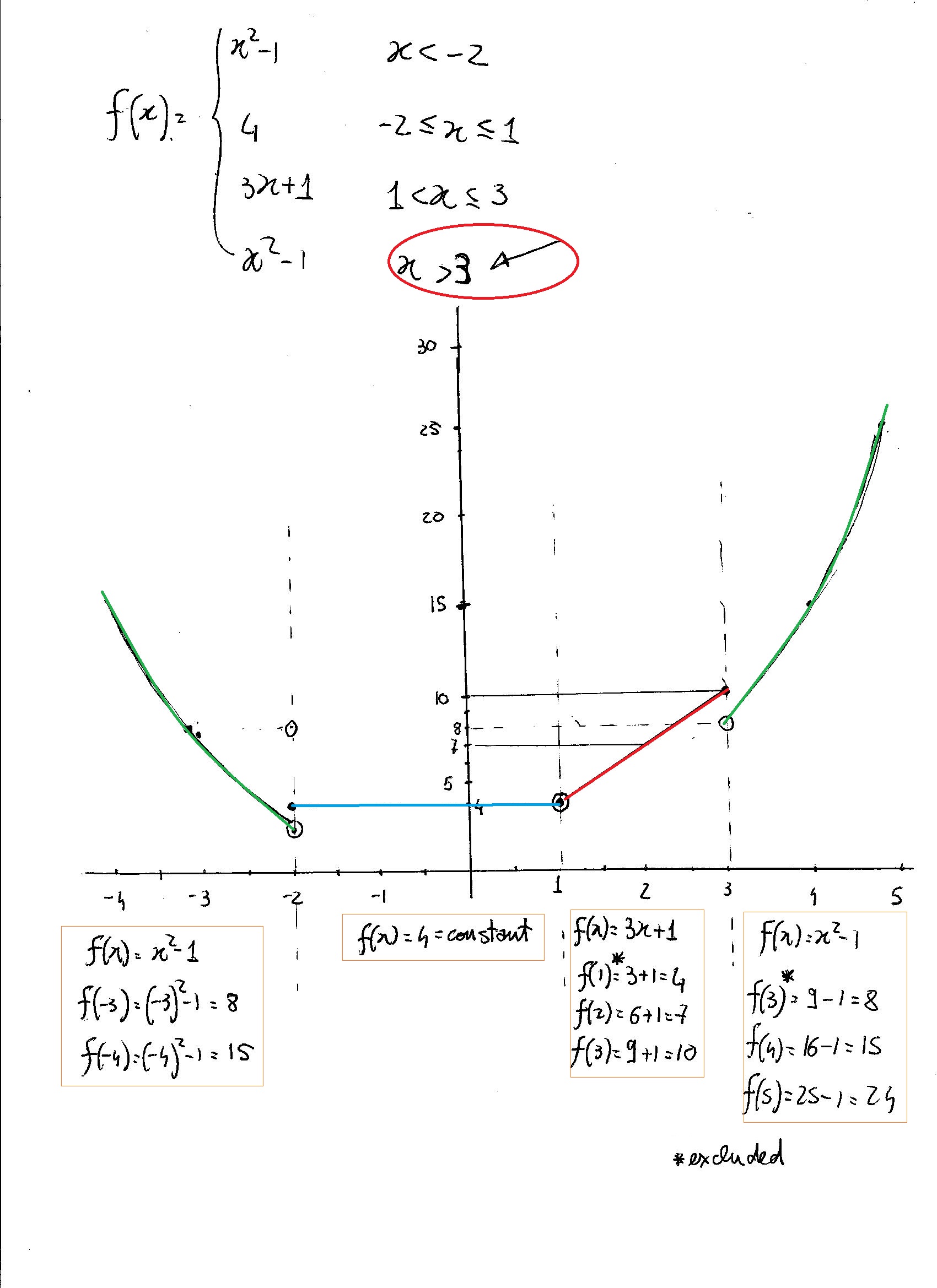



How Would You Graph F X If F X X 2 1 X 2 4 2 X 1 3x 1 1 X 3 X 2 1 X 1 How Would You Evaluate The Function At The Indicated Points F 3 F 2 F 5 F 3 Socratic



Search Q X 5e2 Graph Tbm Isch
Graph exponential and log functionsQuestion Let f(x)= 3x If g(x)is the graph of f(x) shifted right 4 units, write a formula for g(x) g(x)= ? The function f(x) = x^3 2x^2 4x 3 is a polynomial function of degree 3 and hence will have three solutions and hence 3 xintercepts The function g(x) has xintercepts at x = 2, x = 1, x = 1 and x = 3
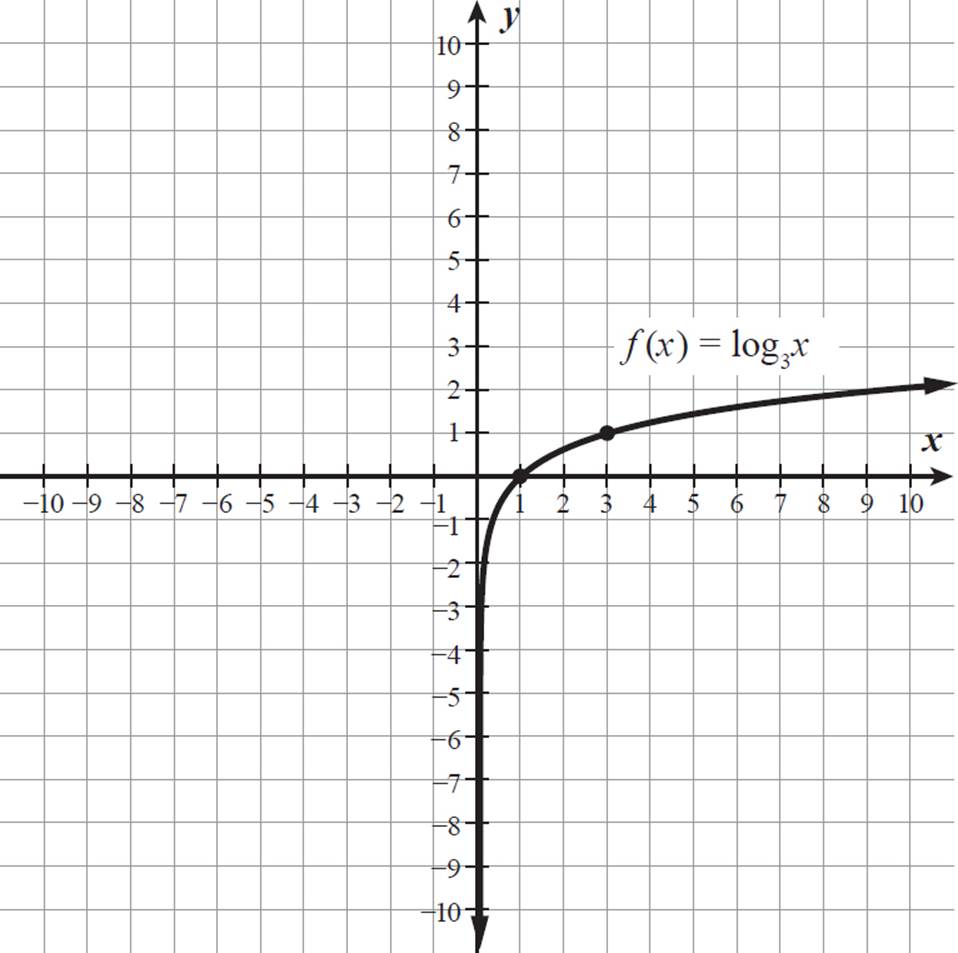



Logarithmic Functions Logarithms High School Algebra Ii Unlocked 16




Which Graph Represents The Function F X X 1 3 Brainly Com
The Function which squares a number and adds on a 3, can be written as f (x) = x2 5 The same notion may also be used to show how a function affects particular values Example f (4) = 4 2 5 =21, f (10) = (10) 2 5 = 105 or alternatively f x → x2 5 The phrase "y is a function of x" means that the value of y depends upon the value ofY=f(x) The x is to be multiplied by 1 This makes the translation to be "reflect about the yaxis" while leaving the ycoordinates alone y=1/2 f(x/3) The translation here would be to "multiply every ycoordinate by 1/2 and multiply every xcoordinate by 3" y=2f(x)5 There could beCalculus Using the first and second derivatives, sketch the graph of f(x) = (x2)/(x1)
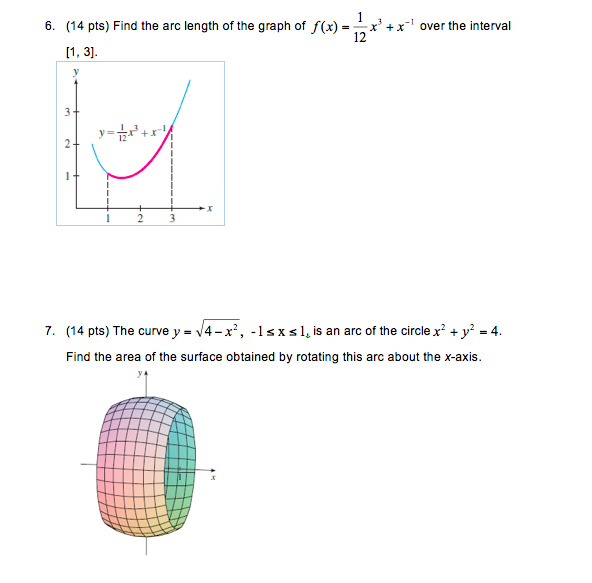



Find The Arc Length Of The Graph Of F X 1 12 X 3 Chegg Com




Without Plotting Any Points Other Than Intercepts Draw A Possible Graph Of The Following Polynomial Brainly Com
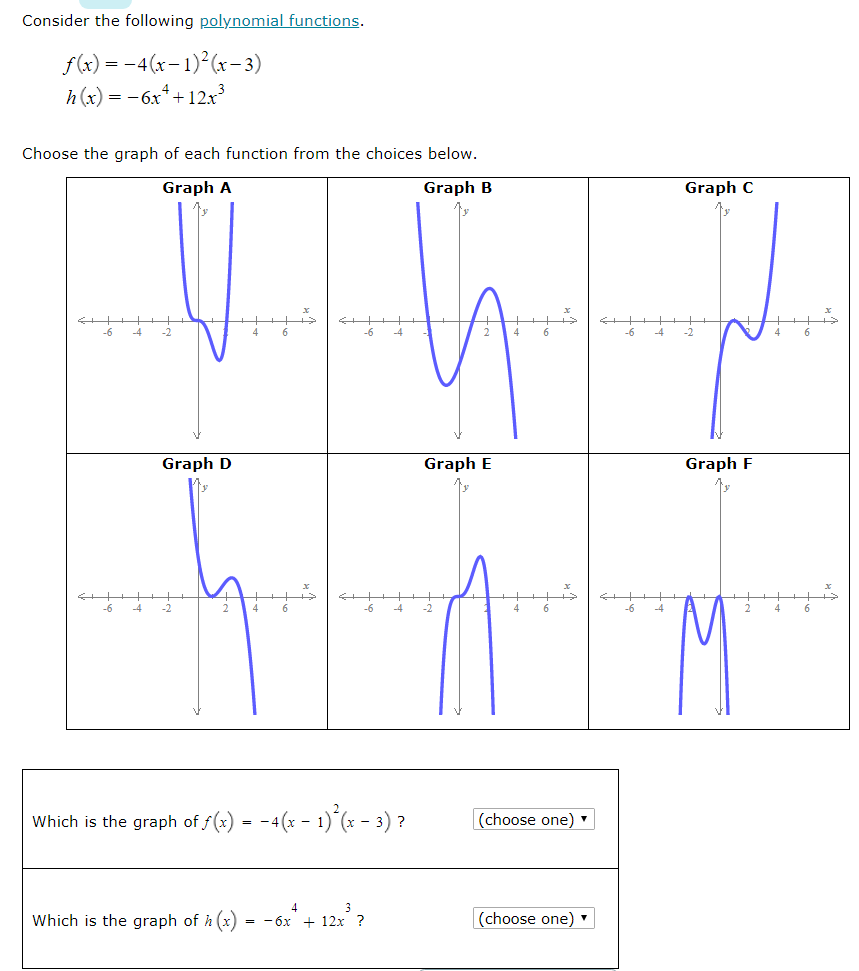



Consider The Following Polynomial Functions Chegg Com




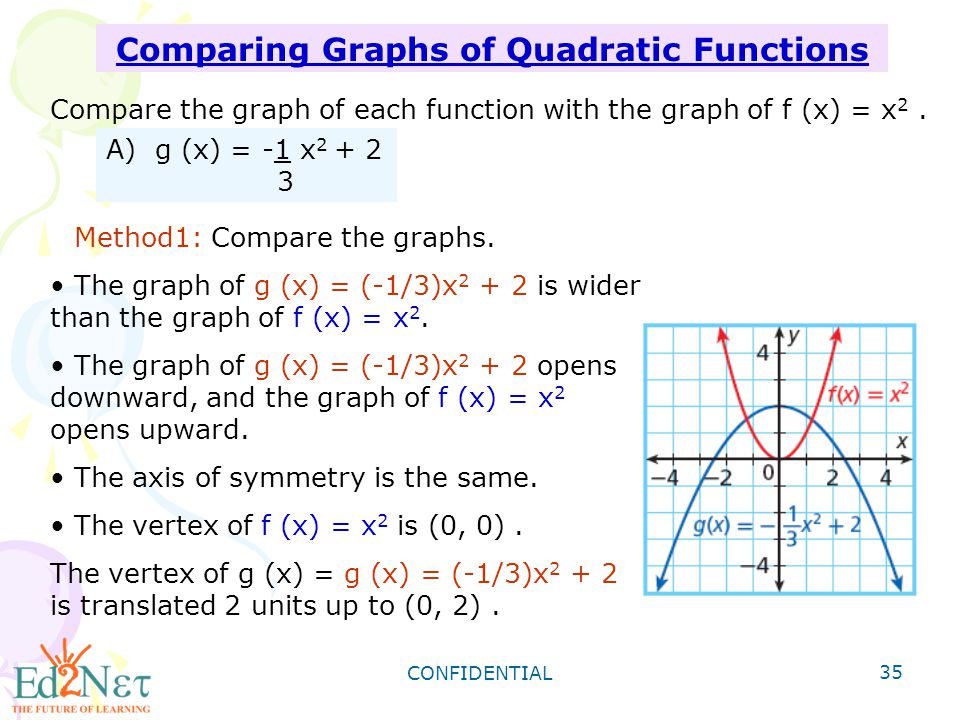
1 G X X G X X 2 2 3 G X 2 0 2x 4 G X 2 X 2 5 G X 2 2 X 2 2 Algebra Ii Ppt Download




Which Graph Represents The Function F X 1 3 X Please Help I Might Fail Brainly Com



Graphing Transformations Of Logarithmic Functions College Algebra



Curve Sketching Example Y X 2 3 6 X 1 3 Youtube



Search Q X 3d3 Graph Tbm Isch



Cages




Which Graph Represents Function F F X 1 3 X Brainly Com
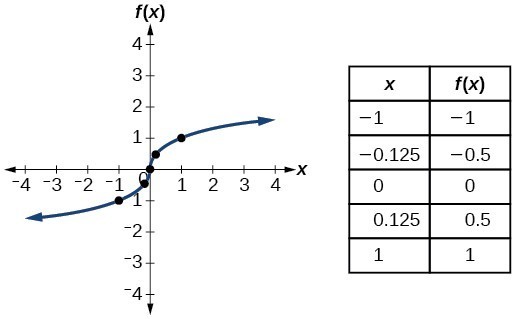



Identify Functions Using Graphs College Algebra



Chapter 6 Exponential And Logarithmic Functions And Applications Section Ppt Download




What Is The Equation Of The Function Shown In The Graph Given That The Equation Of The Parent Brainly Com



Solution How Do You Graph F X 1 3 X




Which Graph Represents The Function F X 1 3 X Brainly Com
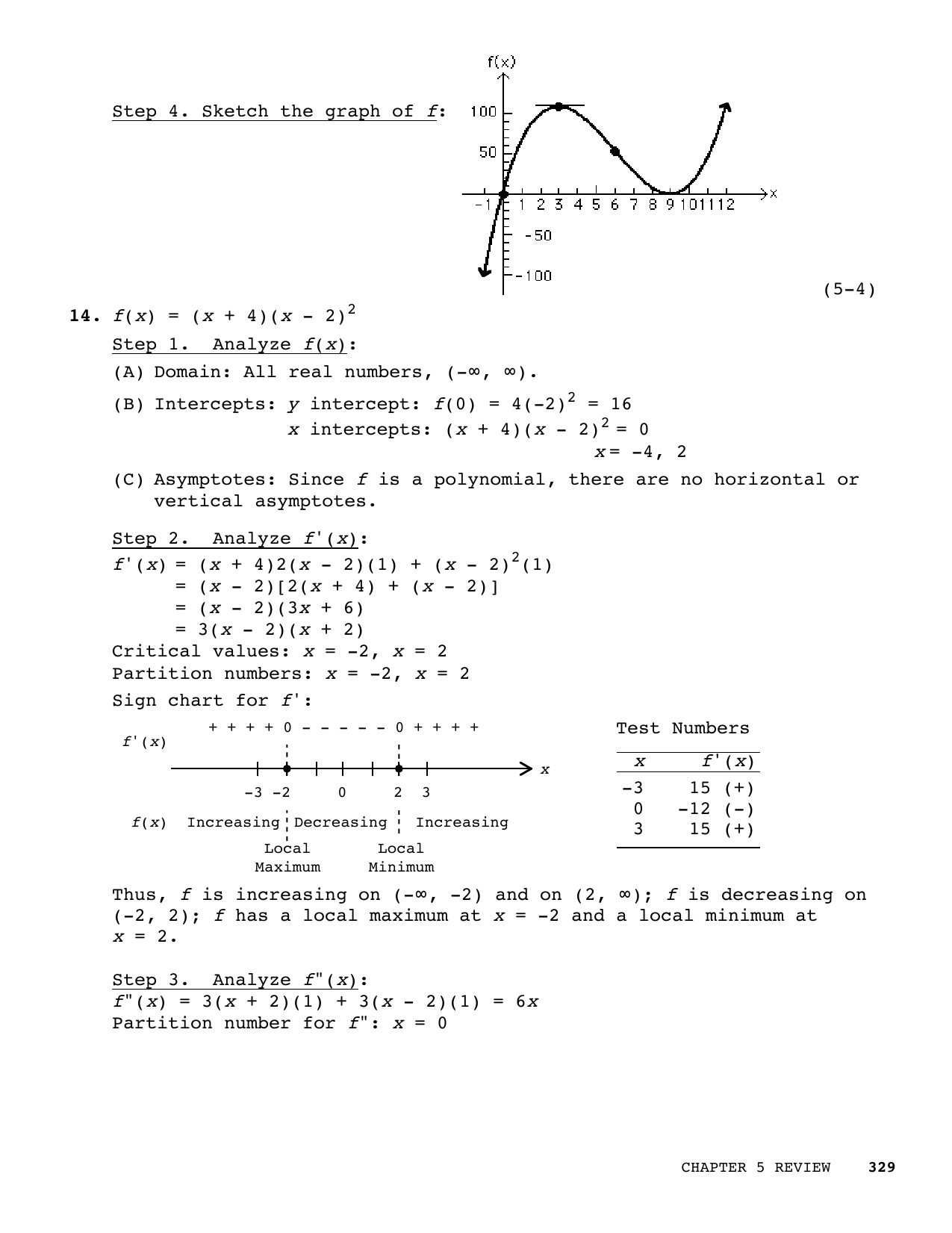



Step 4 Sketch The Graph Of F 5 4 14 F X X 4 X Manualzz
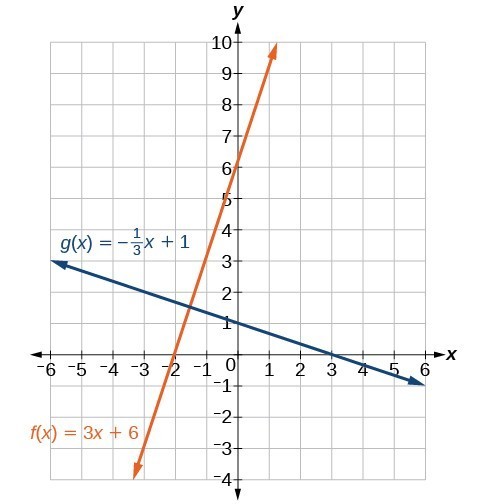



Write The Equation Of A Line Parallel Or Perpendicular To A Given Line College Algebra
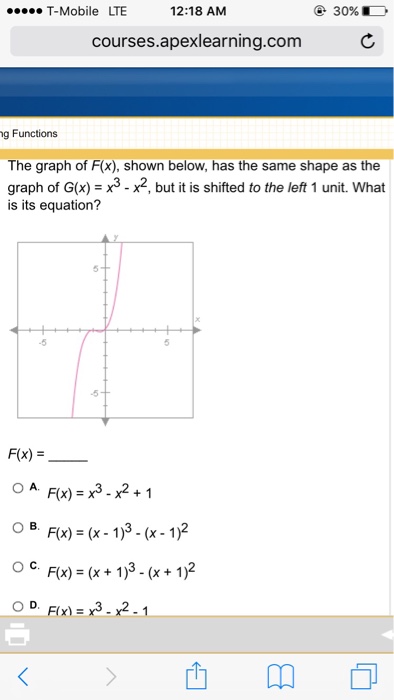



The Graph Of F X Shown Below Has The Same Shape As Chegg Com



One To One Functions
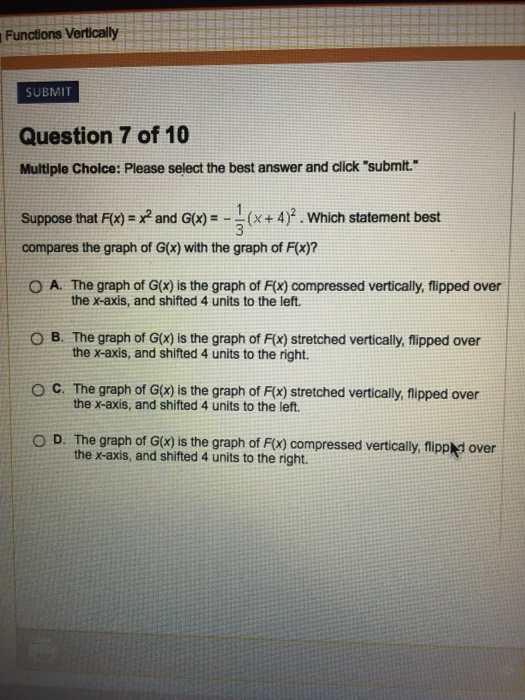



Suppose That F X X 2 And G X 1 3 X 4 2 Which Chegg Com
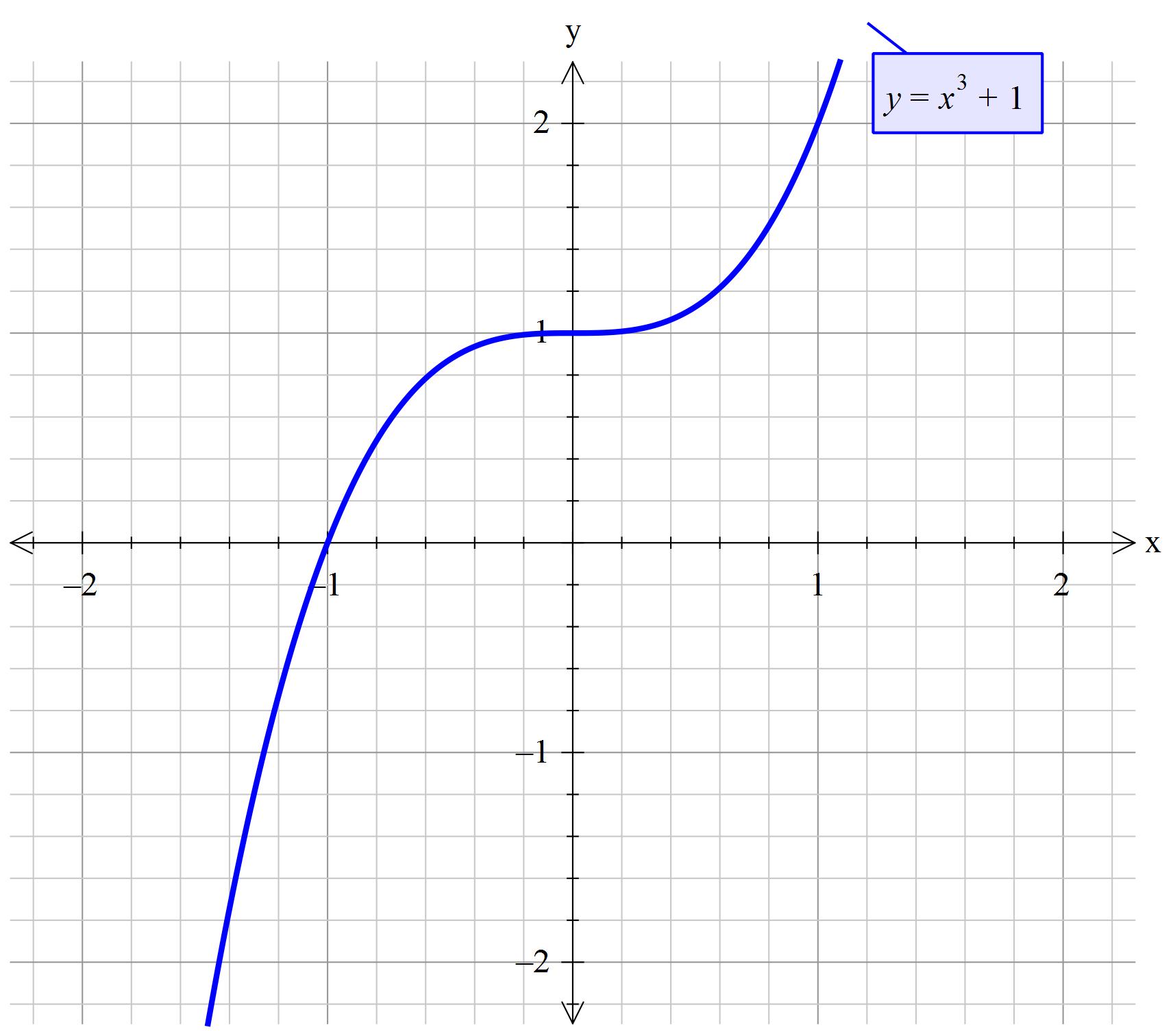



How Do You Sketch The Graph F X X 3 1 Socratic



Sites Levittownschools Com Cbergersen Documents Unit 2 hw answers Pdf
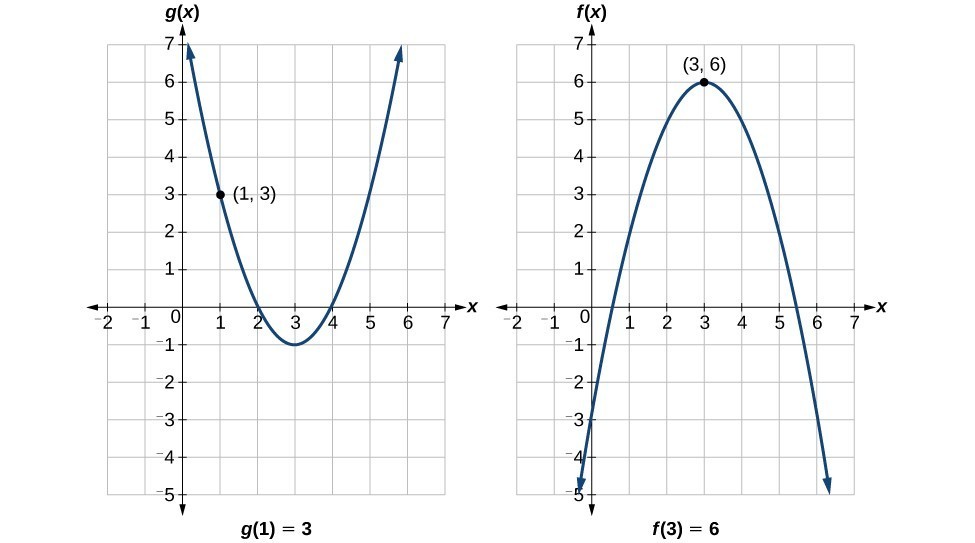



Evaluate Composite Functions College Algebra
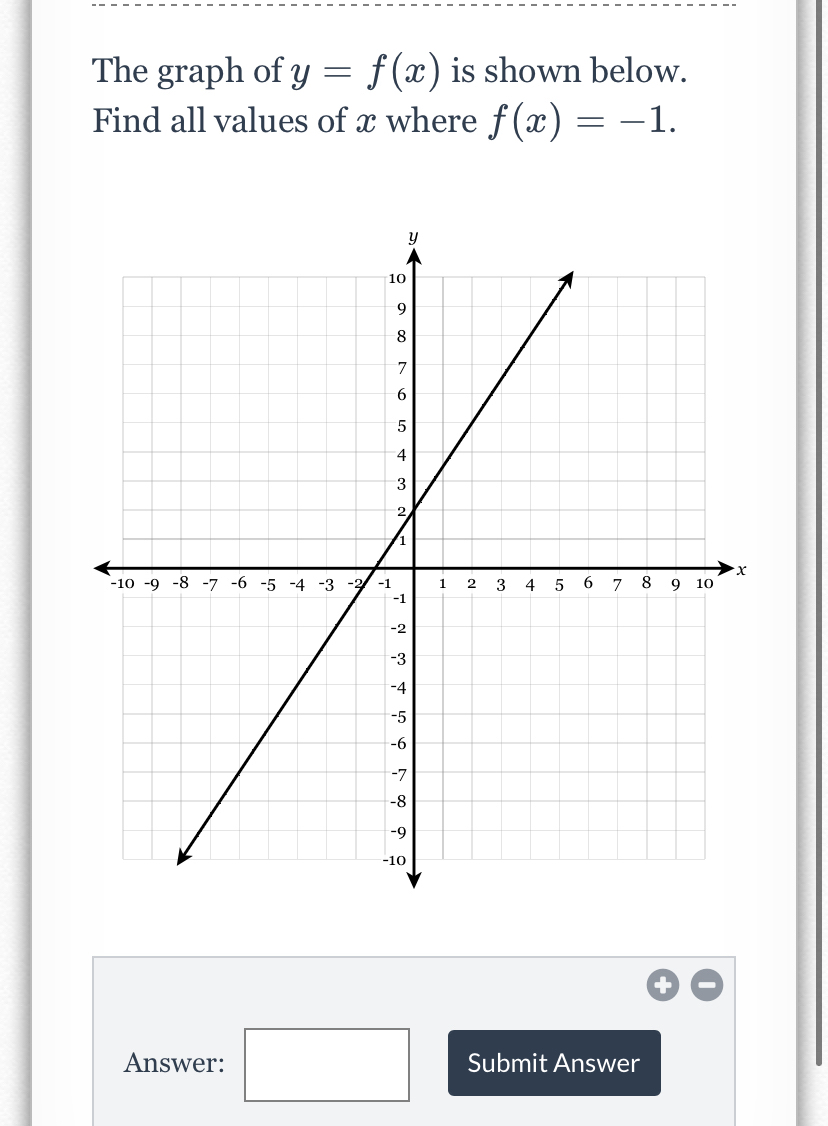



Answered F X Is Shown Below The Graph Of Y Bartleby



Trigonometry Graphing Trigonometric Functions



How Do You Find The Domain And Range Of T 1 3 Socratic




Match The Function With Its Graph 1 F X 4 3 X 2 2 F X 4 3 X 1 2 3 F X 4 3 X 2 1 4 F X 3 X 1 5 F X 3 X 1 6 F X 3 X 1 2 Study Com



Modulus Function
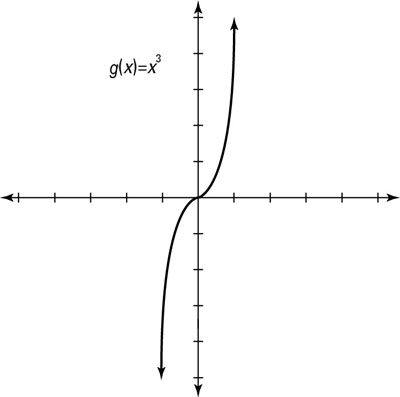



How To Graph Parent Functions Dummies
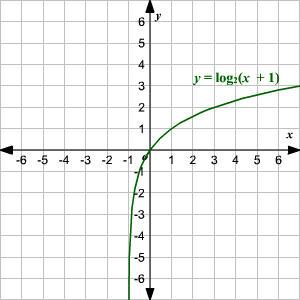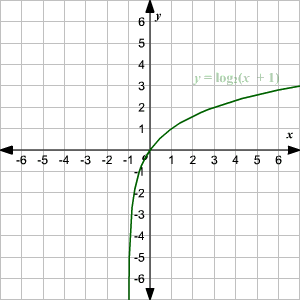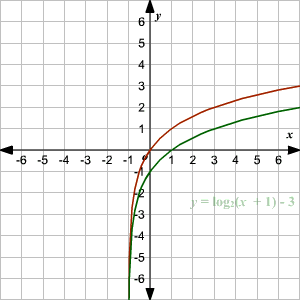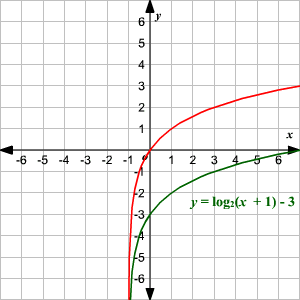



Graphing Logarithmic Functions
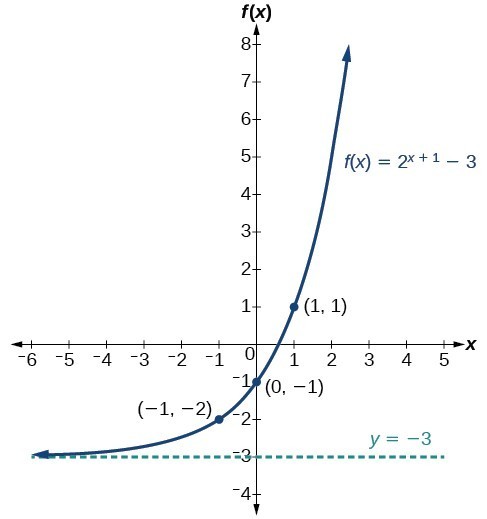



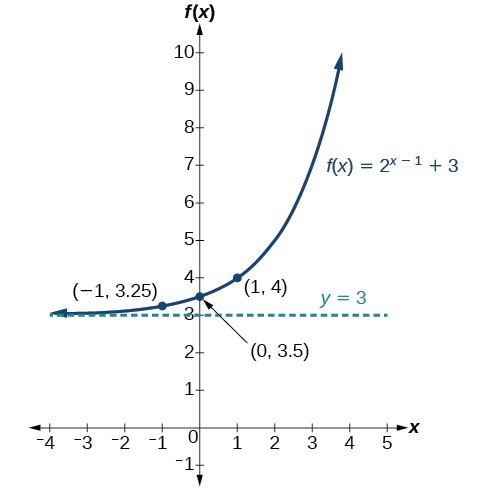
Graph Exponential Functions Using Transformations College Algebra



How Do You Sketch The Graph Of Y 2 Cot 1 3 X Over The Interval 0 6pi Socratic
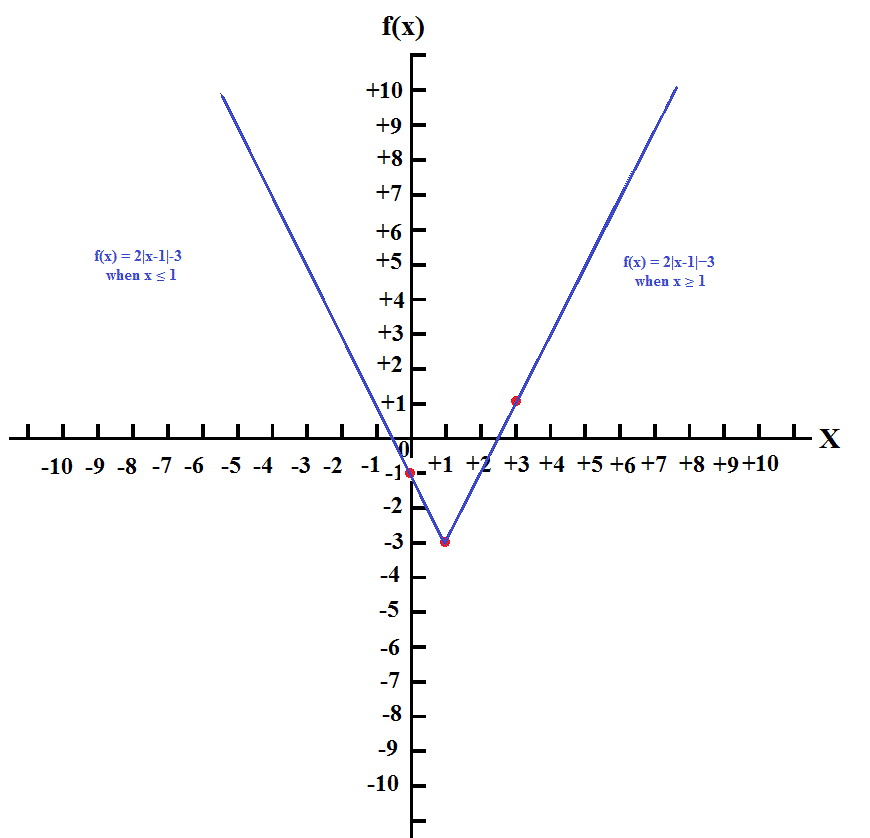



How Do You Graph F X 2abs X 1 3 Socratic
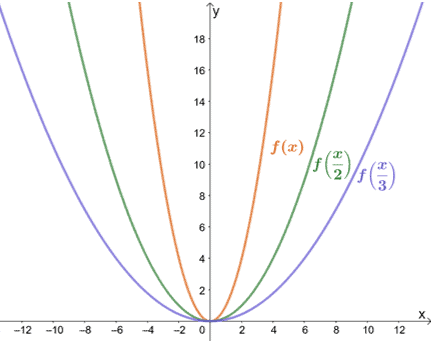



Horizontal Stretch Properties Graph Examples



Solving Equations Graphically



Solution Graphf X X 4 F X X 4 F X X 4 5 F X X 5 4 F X 3x 4 F X 1 3 X 4




The Functions F X 2x 2 And G X 1 3 X 1 Are Shown In The Graph What Are The Solutions To Brainly Com




2 Consider The Graph Of The Function F X 1 X 1 3 2 Chegg Com
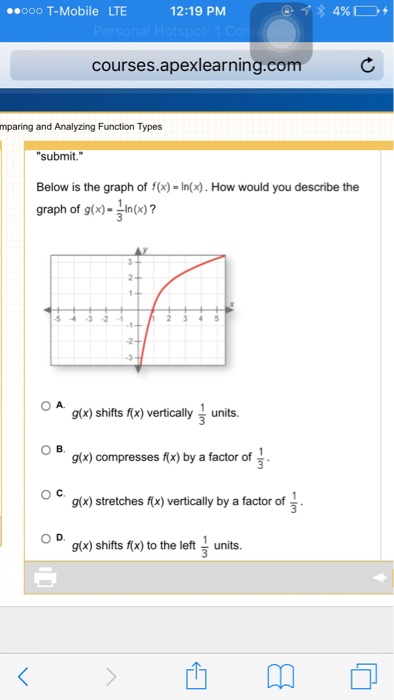



Below Is The Graph Of F X Ln X How Would You Chegg Com
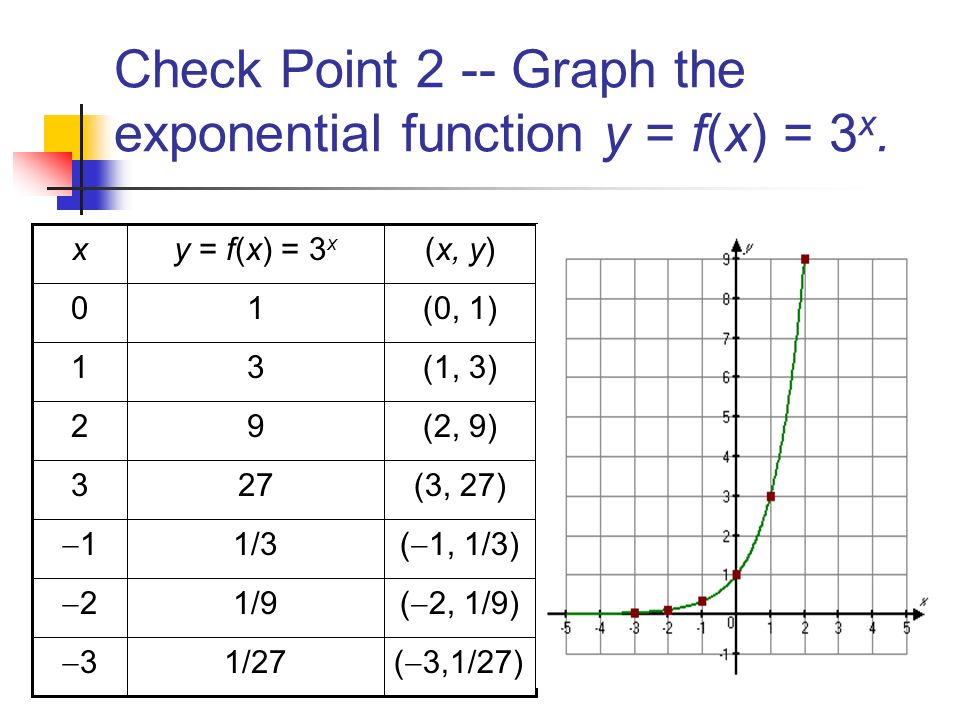



Lesson 3 1 Page 376 Exponential Functions Objective To Graph Exponentials Equations And Functions And Solve Applied Problems Involving Exponential Functions Ppt Download




Which Is The Graph Of F X 3 2 1 3 X Brainly Com



Graph Of Z F X Y Geogebra




How To Graph An Exponential Function F X 1 3 X Youtube
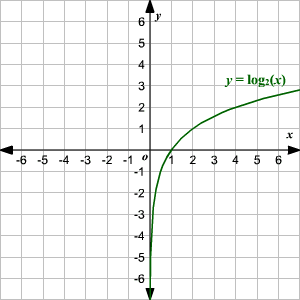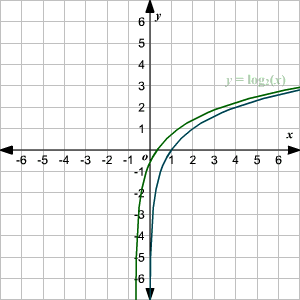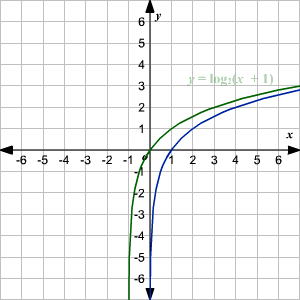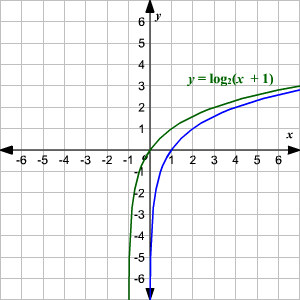



Graphing Logarithmic Functions
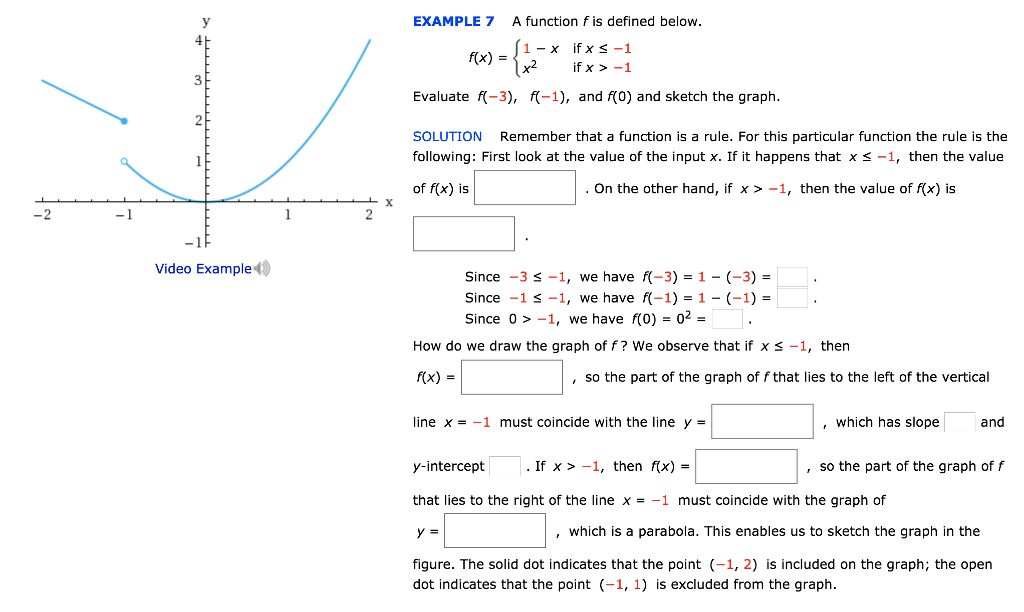



Example 7 A Function F Is Defined Beloww 1 X If X Chegg Com



Solution Find The Inverse Of The Function F X X 1 3 2 I Am So Confused Can Someone Please Help Me Fr A X 2 3 B X 1 3 2 C Y 2 3 D Doesn 39 T Exist
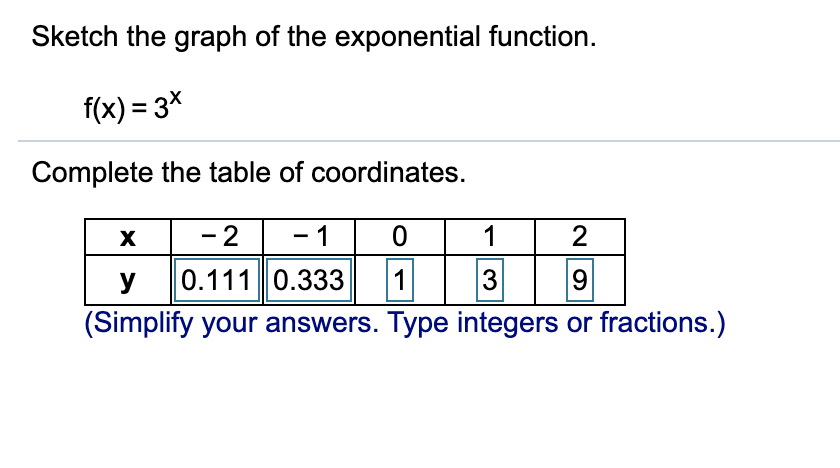



Sketch The Graph Of The Exponential Function F X Chegg Com




Using Transformations To Graph Functions




Sketch The Graph The Given Function F X 2 X If X Chegg Com




Lesson 1 1 Pages 5 11 State The Domain And Range Of Each Relation Then State Whether The Relation Is A Function Write Yes Or No Pdf Free Download



Answer In Algebra For Dani Wagas




Graph The Function Y 1 3 X Then Use Its Graph To Chegg Com



Http Www Mpsaz Org Rmhs Staff Lxcoleman Trig Test Practice Files Review Chapter 3 Notes Solutions Pdf



Describe End Behaviors Consider The Functions F X Chegg Com




Graph F X 1 3 X And G X Log 1 3x In The Same Chegg Com
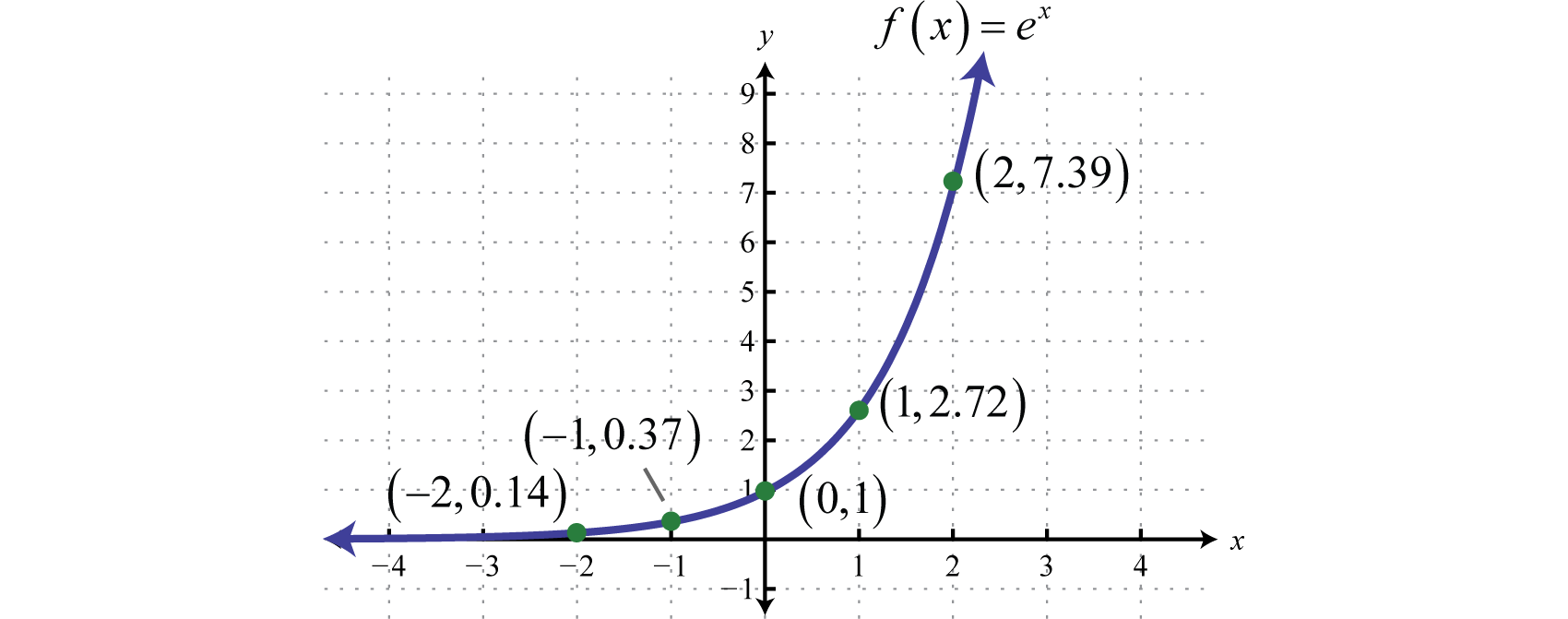



Exponential Functions And Their Graphs



Solution Please Help Graph The Function Quot F X Quot System Matrix 1 3 X If X Gt 2 Matrix 1 3 X 4 If X Lt 2



Skills In Txercises 1 4 Match The Quadratie Chegg Com



Solution If F X 1 3 X And A Lt B Which Of The Following Must Be True A F A F B 3 B F A 1 3 F B C F A F B



Http Media Collegeboard Com Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf




Differentiable



Http Media Collegeboard Com Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf




Graph A Rational Function
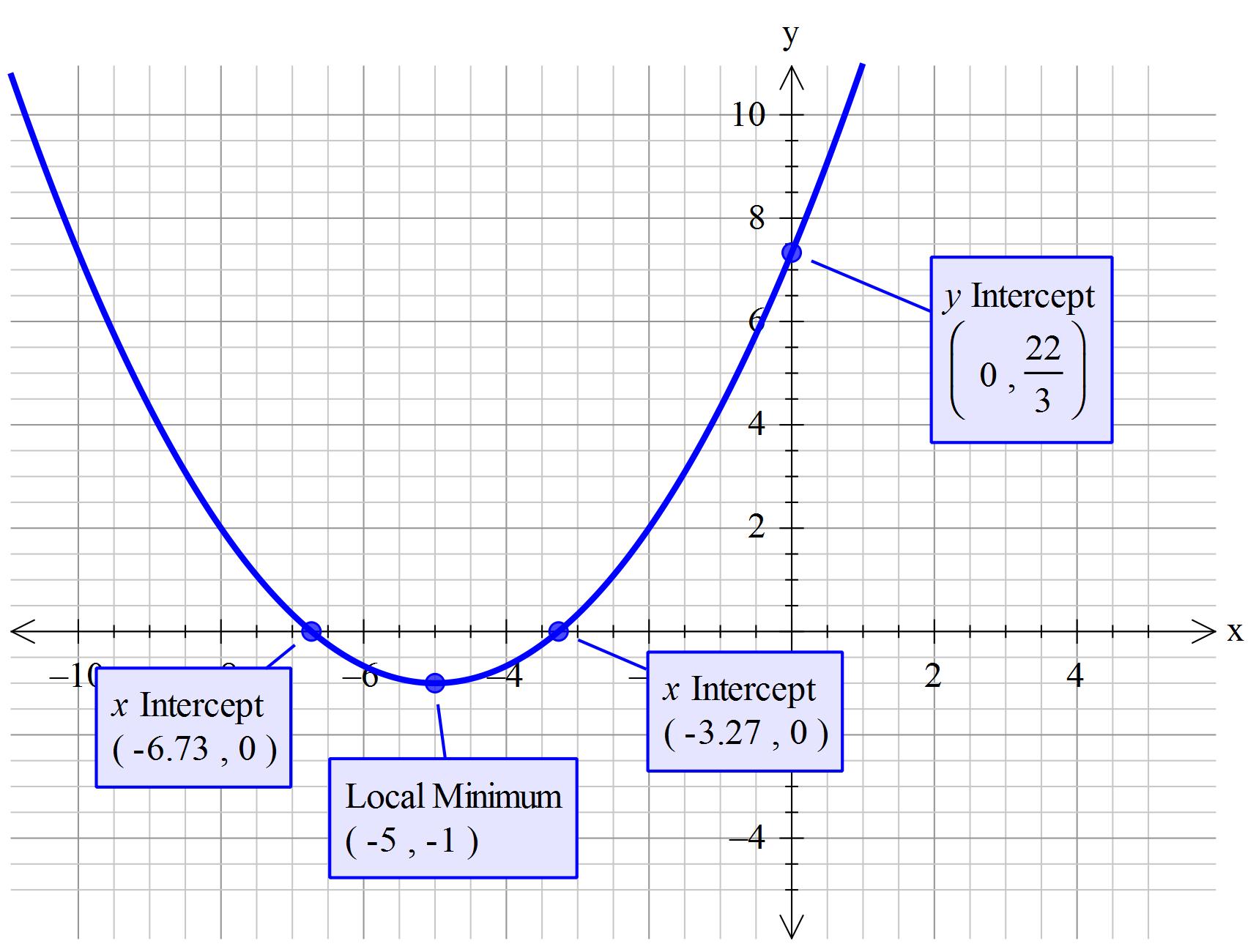



How Do You Use The Important Points To Sketch The Graph Of F X 1 3 X 5 2 1 Socratic




If F X X3 And G X X 1 3 Which Is The Graph Of G X Brainly Com



Www Math Utah Edu Wortman 1050 Text If Pdf
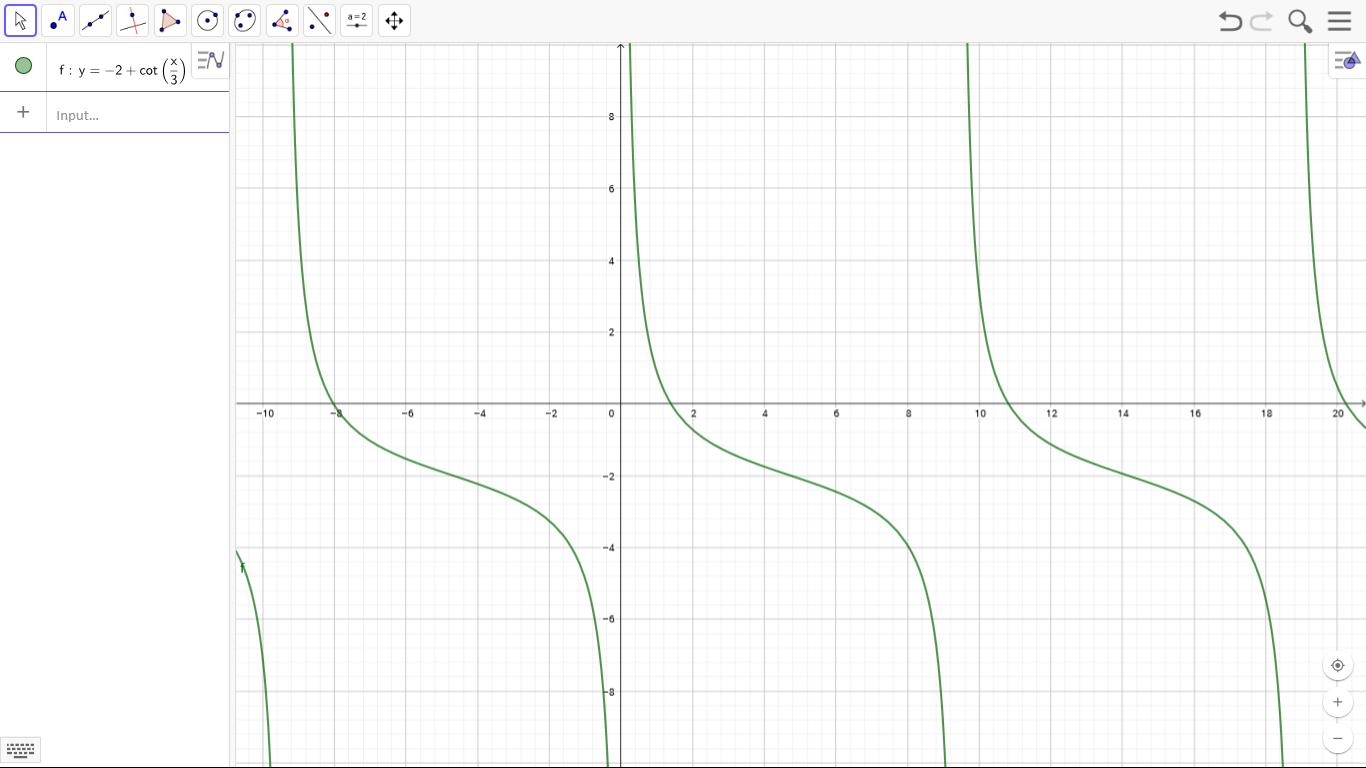



How Do You Sketch The Graph Of Y 2 Cot 1 3 X Over The Interval 0 6pi Socratic
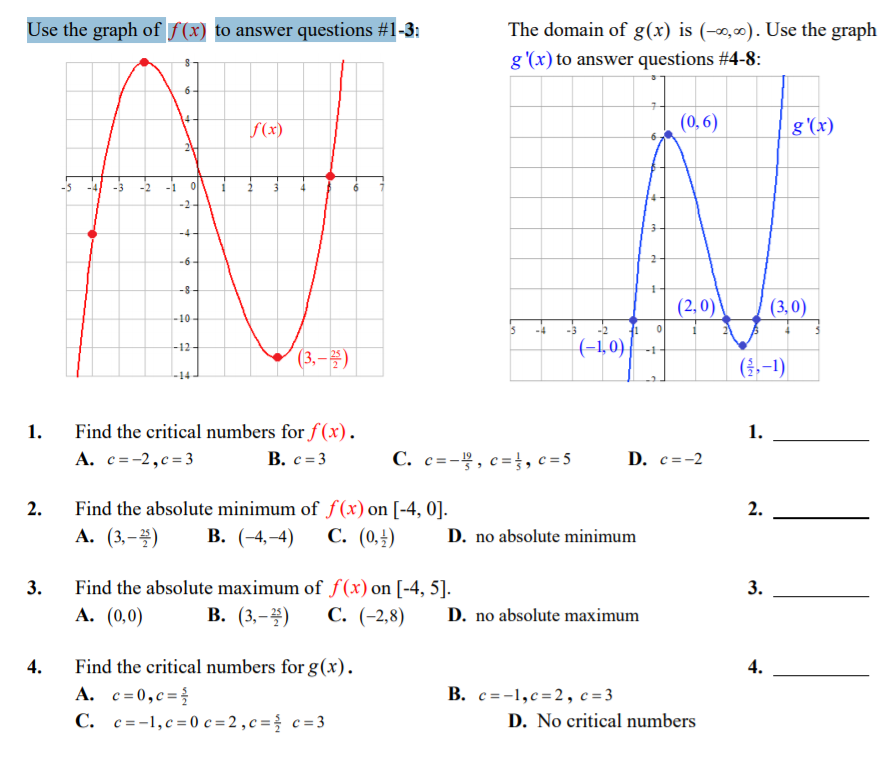



Use The Graph Of F X To Answer Questions 1 3 The Chegg Com
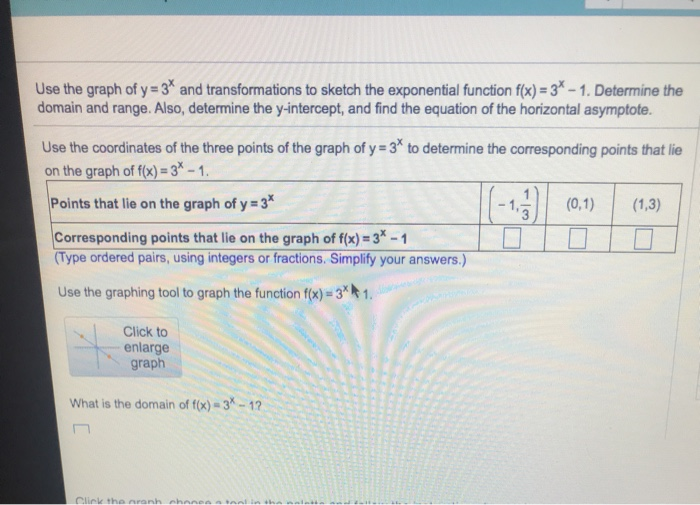



Use The Graph Of Y 3 And Transformations To Sketch Chegg Com



Assignment 6 Solutions




Which Is The Graph Of F X 3 2 1 3 X Brainly Com
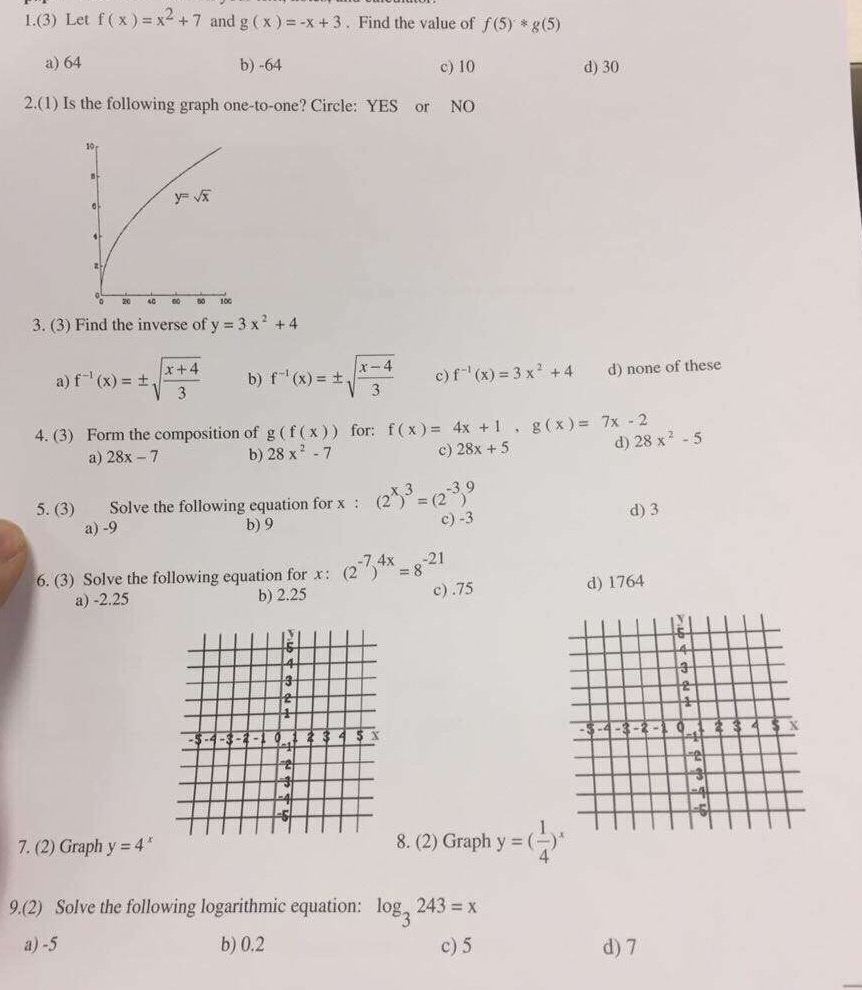



1 3 Let F X X2 7 And G X X 3 Find The Chegg Com



Www Humbleisd Net Cms Lib2 Tx Centricity Domain 3611 Answer review final exam fall Pdf



How Do You Compare The Graph Of M X 5x To The Graph Of F X X Socratic
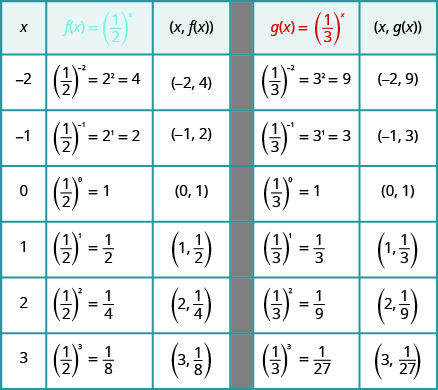



10 3 Evaluate And Graph Exponential Functions Mathematics Libretexts




Which Graph Best Represents The Function F X X 1 X 3 X 3 Brainly Com



No comments:
Post a Comment